平均、平方和、分散、標準偏差を求める
平均、平方和、分散、標準偏差を求めます。データは int data[30] = {6,3,5,9,8,1,2,10,4,3,7,4,3,7,6,5,3,4,5,8,1,4,9,2,4,5,3,7,6,5};
を使用します。
平均値とは、データの総和をデータの個数で割った値のことで、全データのだいたい真中の値を表します。データの個数をn、個々のデータを  として、平均値を式で表すと以下のようになります。
として、平均値を式で表すと以下のようになります。
 (平均値)
(平均値)
平方和とは、個々のデータと平均値の差を二乗した値の和のことで、データが全体的にどの程度ばらついているかを表します。平方和が大きいとばらつきが大きい、平方和が小さいとばらつきが小さいといえます。
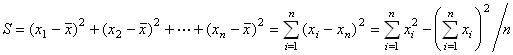 (平方和)
(平方和)
平方和はばらつきを示す尺度ですが、データの数が多くなるとその値は大きくなります。これではデータの個数が異なるもののばらつきを平方和では比較することができません。
そこで平方和をデータの数で割ってばらつきを平均化しようとする統計量が分散です。分散はデータ1つ当たりどの程度ばらついているかを示しているので、データの個数が異なるもののばらつきを比較することができます。 下の式は平方和をデータの個数ではなく、(データの個数−1)で割っています。これは統計学においてnより(n-1)で割るほうが都合のよいためです。統計学ではn-1で割るほうが一般的です。
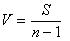 (分散)
(分散)
分散は確かに値の大小によりばらつきの比較はできますが、分散の値自体がデータのばらつきの程度とどう関係があるのか直感的に把握できません。例えば分散が32であるといわれても、データがどの程度ばらついているか直感がわきません。
そこで、値の大小だけでなく、その値自体がどの程度データがばらついているかを示している統計量も必要です。それが標準偏差です。標準偏差は分散にルートをつけるだけで求めることができます。これにより、平方和でばらつき(平均値とデータの値の差)
を2乗した分を元に戻すことができるので、標準偏差の値はデータ1つ当たりのばらつきの平均値に近い値であるということができます。
 (標準偏差)
(標準偏差)
平均、平方和、分散、標準偏差を求めるプログラムは以下のようになります。
<サンプルプログラム>
/****************************************************************************/
#include<stdio.h>
#include<math.h>
int main()
{
// 変数定義
int data[30] = {6,3,5,9,8,1,2,10,4,3,
7,4,3,7,6,5,3,4,5,8,
1,4,9,2,4,5,3,7,6,5};
double ave, squ, v, s;
int i, data_num;
double sum = 0.0, sumv = 0.0;
// 変数の初期化
ave = 0.0;
squ = 0.0;
v = 0.0;
s = 0.0;
i = 0;
data_num = 30;
sum = 0.0;
sumv = 0.0;
// データの総和と二乗和を計算する
for(i = 0; i < data_num; i++)
{
sum += data[i]; // データの総和
sumv += data[i] * data[i]; // 二乗和
}
// 平均・平方和・分散・標準偏差を求める
ave = sum / data_num; // 平均
squ = sumv - (sum * sum / data_num); // 平方和
v = squ / (data_num - 1); // 分散
s = sqrt(v); // 標準偏差
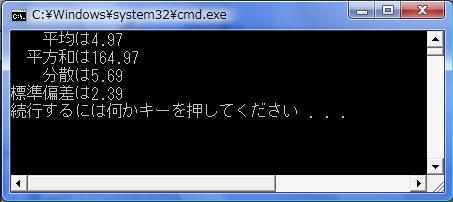
printf(" 平均は%0.2f\n", ave);
printf(" 平方和は%0.2f\n", squ);
printf(" 分散は%0.2f\n", v);
printf("標準偏差は%0.2f\n", s);
return 0;
}
/****************************************************************************/
<実行結果>
<Topページ>
Copyright(c) 2010 , cgengor
このWebページの内容を無断で複製または転載することを禁じます。
このWebページの情報を利用することにより発生したいかなる損害について著作権保有者はいっさいの責任を負いません。
 (平均値)
(平均値)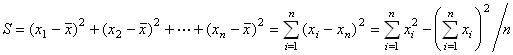 (平方和)
(平方和)