　　C言語例文集

　場合の数（順列、組合せ、重複組合せ）

　高校数学で勉強する順列（Permutation）、組合せ（Combination）、重複組合せ（Homogeneous product）を求めるプログラムを作成します。

＜順列の公式＞

＜組合せの公式＞

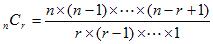
＜重複組合せの公式＞

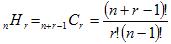
公式だけではわかりにくいので例題を以下に示します。

【例題】
　ここはある中学校です。あるクラスのある班に6人（Aさん、Bさん、Cさん、Dさん、Eさん、Fさん）の生徒がいます。

問1：この6人の中から班長1人、副班長1人、書記1人を選ぶ方法は何通りありますか？
問2：この6人を一列に並べる方法は何通りありますか？
問3：この6人の中から掃除係2人を選ぶ方法は何通りありますか？
問4：この6人を3人と3人の2グループに分ける方法は何通りありますか？
問5：この6人を2人、2人、2人の3グループに分ける方法は何通りありますか？
問6：同じ種類の8個のチョコを6人で分ける方法は何通りありますか？（チョコを1個ももらわない人がいても良い）
問7：同じ種類の8個のチョコを6人で分ける方法は何通りありますか？（各人必ずチョコを最低1個もらうものとする）

＜解答＞
●問1
班長を選ぶ方法はＡ、Ｂ、Ｃ、Ｄ、Ｅ、Ｆのいずれかなので6通り、副班長を選ぶ方法は班長以外の5人から選ぶので5通り、書記を選ぶ方法は班長、副班長以外の4人から選ぶので4通りとなる。

そのため
₆P₃ ＝6×5×4 ＝ 120
より、120通りが答えとなる。

以下のような、樹形図で考えるとわかりやすいと思います。

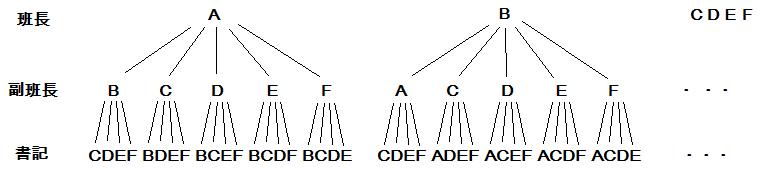
●問2
問1と考え方は同じです。先頭の人を選ぶ方法は6通り、2番目は5通り、3番目は4通り、4番目は3通り、5番目は2通り、6番目は1通りとなる。

そのため
₆P₆ ＝6×5×4×3×2×1＝ 720
より、720通りが答えとなる。

●問3
並べる順序を気にする必要が無いため（ABとBAは同じと考えることができるため）組合せの問題となる。
6人の中から2人を選ぶので、

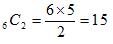
より、15通りが答えとなる。列挙すると以下の通り。
(A,B)、(A,C)、(A,D)、(A,E)、(A,F)、(B,C)、(B,D)、(B,E)、(B,F)、(C,D)、(C,E)、(C,F)、(D,E)、(D,F)、(E,F)

●問4
考え方は問3と同じです。6人の中から3人を選べば良い(2グループ目は自動的に残りの3人となるので計算する必要はない)ので、

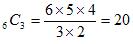
より、20通りが答えとなる。

●問5
6人の中から2人を選び、さらに残りの4人の中から2人を選べば良いので、

より、90通りが答えとなる。

●問6
このような問題はチョコを★と考え、縦棒（｜）をしきりにするとわかりやすいです。
下図は、★×8がチョコ8個を表し、しきり（｜）×5（6人-1）が人を表しています。
例えば一番左がAのもらえるチョコの個数を、右側にひとつしきりを挟んだところがBのもらえるチョコの個数を表します。

★★★★★★★★｜｜｜｜｜　　→　(A,B,C,D,E,F) = (8,0,0,0,0,0)
★★★★★★★｜★｜｜｜｜　　→　(A,B,C,D,E,F) = (7,1,0,0,0,0)
★★★★★★｜★｜｜｜｜★　　→　(A,B,C,D,E,F) = (6,1,0,0,0,1)
★★｜★｜★｜★｜★｜★★　　→　(A,B,C,D,E,F) = (2,1,1,1,1,2)

このように★としきり「｜」の並び方の組合せが、チョコの分け方の組合せを表しているといえるので、

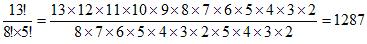
または

で求めることができ、答えは1287通りとなる。

●問7
各人最低1個のチョコをもらうので、まずは6個のチョコを6人にそれぞれ分配し、残りの2個のチョコを問6と同じ考え方で解いていく。

★★｜｜｜｜｜　　→　(A,B,C,D,E,F) = (3,1,1,1,1,1)
★｜★｜｜｜｜　　→　(A,B,C,D,E,F) = (2,2,1,1,1,1)
｜★｜｜｜｜★　　→　(A,B,C,D,E,F) = (1,2,1,1,1,2)

または

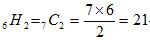
で求めることができ、答えは21通りとなる。

＜サンプルプログラム＞

/****************************************************************************/
#include<stdio.h>
#include<string.h>

int Permutation(int n, int r);  // 順列の関数宣言
int Combination(int n, int r);  // 組合せの関数宣言
int Homogeneous(int n, int r);  // 重複組合せの関数宣言

int main()
{
    fprintf(stdout, "問1：6P3 = %d\n", Permutation(6,3));
    fprintf(stdout, "問2：6P6 = %d\n", Permutation(6,6));
    fprintf(stdout, "問3：6C2 = %d\n", Combination(6,2));
    fprintf(stdout, "問4：6C3 = %d\n", Combination(6,3));
    fprintf(stdout, "問5：6C2 × 4C2 = %d\n", Combination(6,2) * Combination(4,2));
    fprintf(stdout, "問6：6H8 = %d\n", Homogeneous(6,8));
    fprintf(stdout, "問7：6H2 = %d\n", Homogeneous(6,2));

    return 0;
}

// 順列(nPr)を求める関数
int Permutation(int n, int r)
{
    int ans;
    int i;

    // 引数チェック
    if(n < r || n < 0 || r < 0)
    {
        fprintf(stderr, "数値が正しくありません\n");
        return -1;  // 強制終了
    }

    ans = 1;

    for(i = 0; i < r; i++)
    {
        ans *= n;
        n -= 1;
    }
    return ans;
}

// 組合せ(nCr)を求める関数
int Combination(int n, int r)
{
    int ans;
    int i;

    // 引数チェック
    if(n < r || n < 0 || r < 0)
    {
        fprintf(stderr, "数値が正しくありません\n");
        return -1;  // 強制終了
    }

    ans = 1;

    for(i = 0; i < r ; i++)
    {
        ans *= n;
        n -= 1;
    }

    for(i = 1; i <= r; i++)
    {
        ans /= i;
    }

    return ans;
}

// 重複組合せ(nHr)を求める関数
int Homogeneous(int n, int r)
{
    int ans;

    // 引数チェック
    if(n < 0 || r < 0)
    {
        fprintf(stderr, "数値が正しくありません\n");
        return -1;  // 強制終了
    }

    ans = Combination(n + r - 1, r);

    return ans;
}
/****************************************************************************/

＜実行結果＞

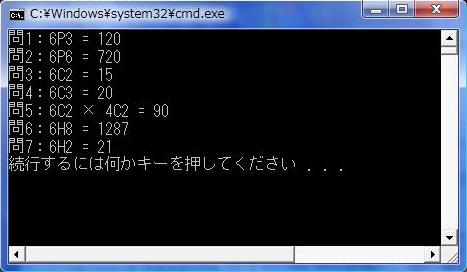
＜Topページ＞